Merkle DAGs: Verifiability
Because we use cryptographic-strength hash algorithms to create CIDs, they offer a high degree of verifiability: an individual who retrieves data using a content address can always compute the CID for themselves to ensure that they got what they were after. This offers both permanence (the data behind a content address will never change) and protection against malicious manipulation (bad actors can’t trick you into downloading the wrong file without you recognizing that it’s not the file you requested).
In a Merkle DAG, the CID of each node depends, in turn, on the CIDs of each of its children. As such, the CID of a root node uniquely identifies not just that node, but the entire DAG of which it’s the root! As a result, we can extend all of the awesome security, integrity, and permanence guarantees of CIDs to our data structure itself, and not just the data that it contains!
Have you ever made a temporary backup copy of a file directory during some editing process, then found the two directories months later and wondered whether their contents were still identical? Rather than laboriously comparing files, you could compute a Merkle DAG for each copy: if the CIDs of the root directory matched, you’d know you could safely delete one and free up some space on your hard drive!
Any Node Can Be a Root Node
DAGs can be seen as recursive data structures, each DAG consisting of smaller DAGs. In our example, the CID "baf...8" identifies a DAG, but so does the CID "baf...6"- it just identifies a smaller DAG, a subgraph of the one identified by "baf...8". The corresponding nodes are both root nodes, given the right context.
This is an extremely powerful and useful property. If we’re retrieving content that’s structured as a DAG, we don’t have to retrieve the entire DAG: we have the option of retrieving a subgraph instead, identified by its own top node’s CID (the top node of this subgraph would become its root node). If we want to share that subgraph with somebody else, we don’t have to include the context of the larger graph we originally retrieved the data from—we just have to send the CID of the subgraph. And, if we want to embed that subgraph as a part of a larger DAG that’s different from the one we originally found it in, we’re free to, because the DAG’s CID, which is the CID of its root node, depends on the root node’s descendents and not its ancestors.
That last point deserves greater emphasis: with Merkle DAGs, we can take the same DAG and seamlessly embed it in multiple other, larger DAGs simultaneously! This enables a massive, interconnected weave of DAGs, building on top of and borrowing pieces from one another.
Ensuring a Root Node Exists
Sometimes, our data doesn’t immediately present a single root node: this is not actually a strict requirement of a DAG. Consider, for example, the following employee hierarchy, which has two managers without any superior and one employee with two managers:
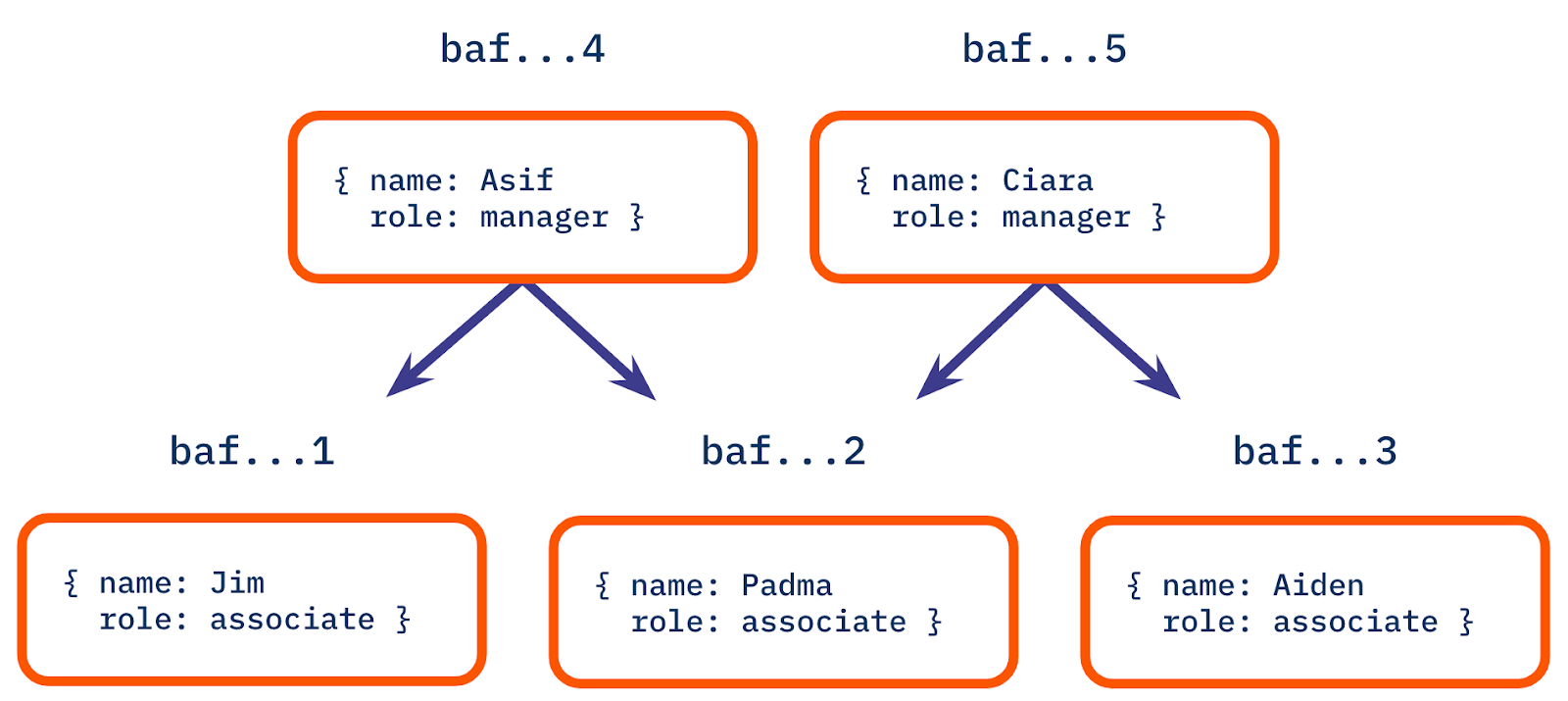
There is no single node that serves as a root node for all five of the nodes in the diagram, and so it would be impossible to share or retrieve the entire DAG using any of baf...1-5. That doesn’t stop us from making one, however! We can create a new DAG by creating an additional node that has the "Asif" and "Ciara" nodes as its own children, and use that as a root node.
Alternatively, we might want to have two separate data structures, where "Asif" or "Ciara" are the respective root nodes (the node for Padma, who has two managers, would be included in both of these DAGs.) The important distinction is that this would make two separate Merkle DAGs, because you cannot navigate to all nodes in this dataset from only one of the two roots (the links in a DAG are directed and there is no link from "Padma" to "Ciara" so you can’t get to either "Ciara" or "Aiden" from a root node of "Asif").
Take the quiz!
When you use content addressing to share or retrieve data arranged in a Merkle DAG...
Feeling stuck? We'd love to hear what's confusing so we can improve this lesson. Please share your questions and feedback.